Bayesian analysis of spiked covariance models: correcting eigenvalue bias and determining the number of spikes (working paper)

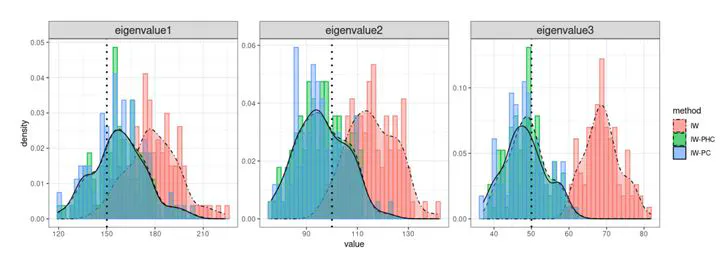
We study Bayesian inference in the spiked covariance model, where a small number of spiked eigenvalues dominate the spectrum. Our goal is to infer the spiked eigenvalues, their corresponding eigenvectors, and the number of spikes, providing a Bayesian solution to principal component analysis with uncertainty quantification. We place an inverse-Wishart prior on the covariance matrix to derive posterior distributions for the spiked eigenvalues and eigenvectors. Although posterior sampling is computationally efficient due to conjugacy, a bias may exist in the posterior eigenvalue estimates under high-dimensional settings. To address this, we propose two bias correction strategies: (i) a hyperparameter adjustment method, and (ii) a post-hoc multiplicative correction. For inferring the number of spikes, we develop a BIC-type approximation to the marginal likelihood and prove posterior consistency in the high-dimensional regime p > n. Furthermore, we establish concentration inequalities and posterior contraction rates for the leading eigenstructure, demonstrating minimax optimality for the spiked eigenvector in the single-spike case. Simulation studies and a real data application show that our method performs better than existing approaches in providing accurate quantification of uncertainty for both eigenstructure estimation and estimation of the number of spikes.