Reflective Hamiltonian Monte Carlo: Mixing Analysis and Application to Sampling on Stiefel Manifold (working paper)

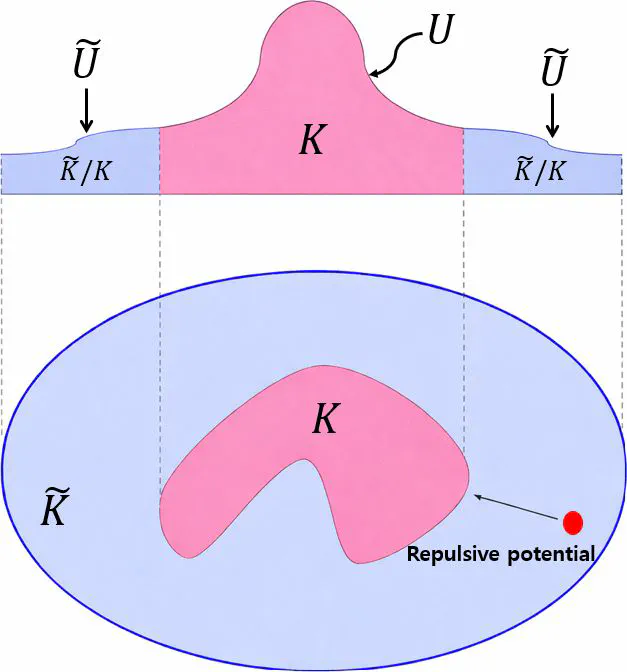
Sampling from distributions with bounded supports is a fundamental challenge in constrained statistical inference. Reflective Hamiltonian Monte Carlo (ReHMC) provides a useful sampling approach for this setting. However, it relies on convexity assumptions on the support and lacks non-asymptotic theoretical guarantees such as mixing-time bounds. To bridge this gap, we propose a convex-container-plus-thinning framework that is applicable to arbitrary target densities with bounded support. We establish the first non-asymptotic total-variation mixing-time bounds for ReHMC, achieving a polynomial dimension dependence of O(d^2) for L-smooth targets, though with exponential dependence on smoothness parameters. Under an additional m-strong convexity assumption, we derive a sharper bound that eliminates this exponential dependence. We further apply this approach to sampling on the Stiefel manifold via a well-conditioned polar reparameterization and demonstrate improved numerical stability and computational efficiency in simulation studies.